A high-order interface is developed under a Centre for Fluid Mechanics Simulation (CFMS) project to link a high-order CAA solver for noise propagation with a high-order CFD solver for near field noise generation. Therefore the interface allows the use of optimal grids for and solvers for each part of an aeroacoustic simulation. Conventional high-order interpolation polynomial functions are adopted to preserve flow disturbances in structured Computational aeroacoustic (CAA) grids with high accuracy. A method is also proposed to account for the effects of complex geometry in the CFD flow domain without physically presenting them in the CAA grids.
Predictions of acoustic wave propagation using methods of computational fluid dynamics (CFD) are expensive in computing cost. This is because the amplitudes of the acoustic waves are several orders lower than mean flow values. In such numerical simulations, the acoustic waves are easily damped or distorted by either numerical dissipation/dispersion or by a stretched grid. In addition to these, in a few flow applications, such as in low Mach number flows, the acoustic waves have large length scales making the CFD flow simulation impropriate for prediction of the acoustic wave propagation due to the fine grid requirement. Therefore high-order computational aeroacoustics (CAA) methods and high-order interface with CFD solutions are essential away from the viscous areas for accurate flow noise prediction in the farfield.
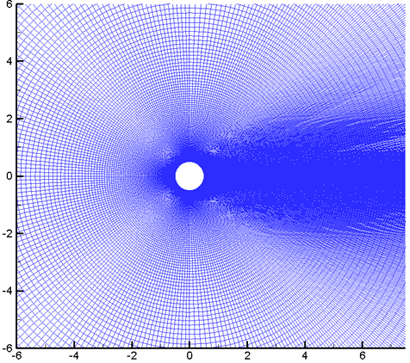
Figure 1: Non-uniform CFD grid for near field prediction.
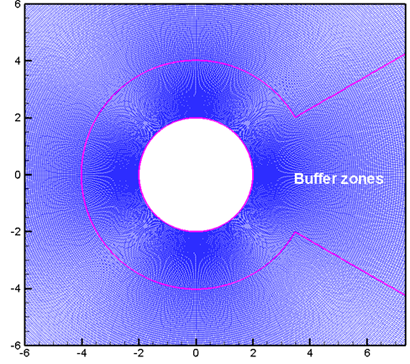
Figure 2: Uniform CAA grid, cylinder geometry excluded in buffer zones
To enable efficient flow noise farfield prediction, CFD generated flow disturbances on structured or unstructured grids are interpolated through high-order polynomial functions into structured CAA grids. With this accurately interpolated noise data, noise propagation in the nearfield and farfield are efficiently predicted through a high-order CAA solver and a Ffowcs Williams-Hawkings solver. The complex geometry area is replaced by a buffer zone (shown in Figure 2) where history of the CFD flow disturbances due to geometry is stored and used to express geometry effects in the CAA grids.

Figure 2: Acoustic pressures simulated using LEE on CAA grid.
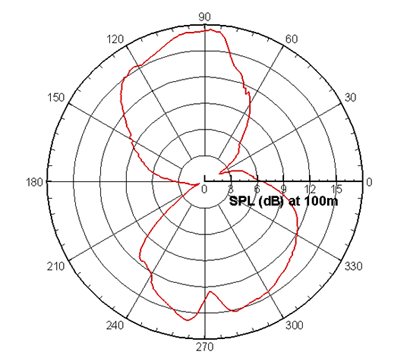
Figure 3: The resulting directivity prediction obtained from the CAA solution
For structured CFD grids the high-order Lagrange’s polynomial function performs well and for unstructured grids a proposed high order polynomial function based on three grid points also provides good performance. In addition a method is proposed to account for the effects of a complex geometry in the CFD flow domain. Through this method the high-order CAA solver can solve general applications where complex geometries exist.